力扣每日一题-动态规划类型题

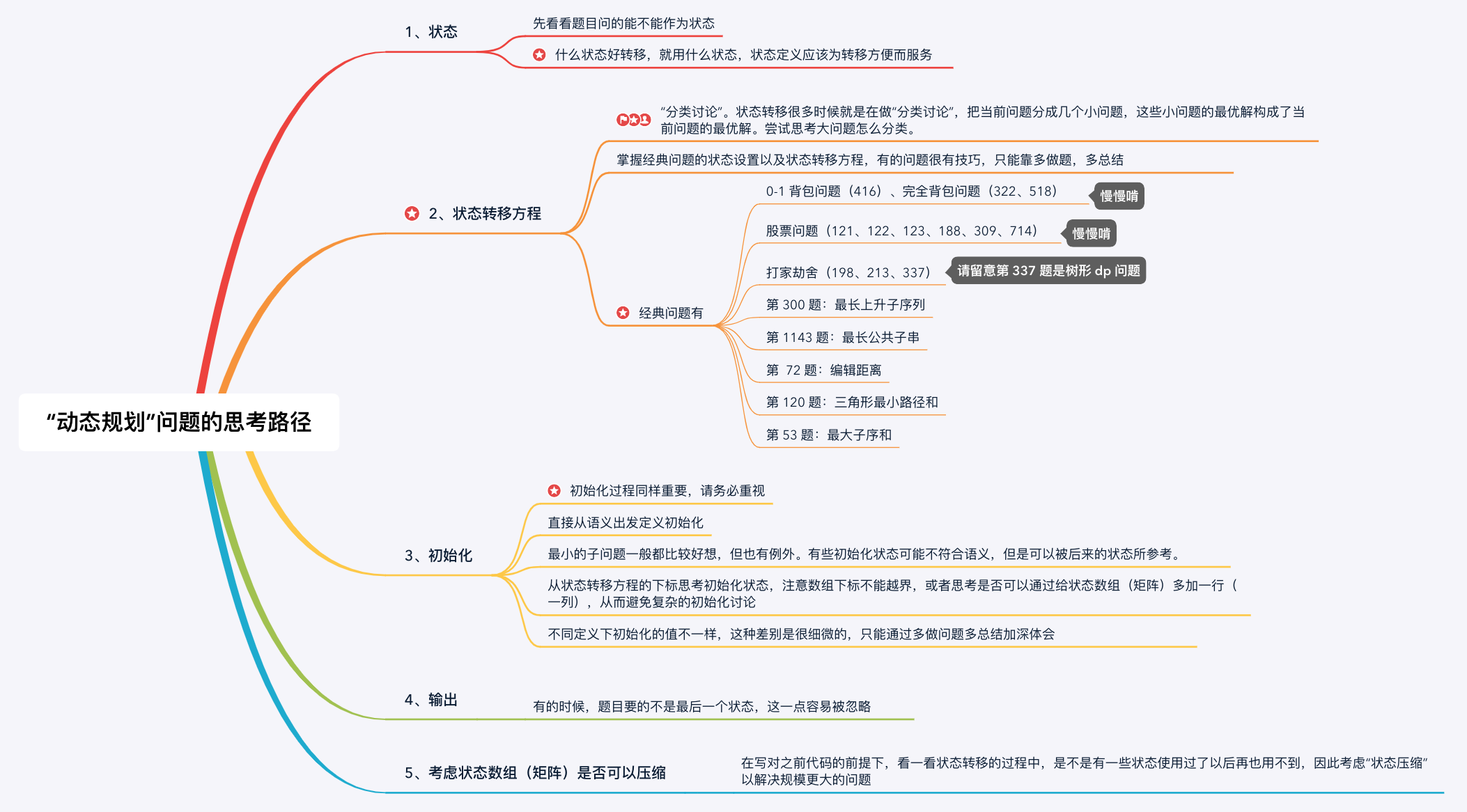
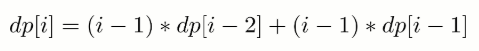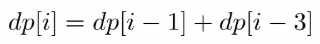动态规划包含三个部分：最优子结构、边界和状态转移方程，审题时应充分思考是否能找出这几部分，也就是看能否进行动态规划的求解。

动态规划的的四个解题步骤是：

• 定义子问题
• 写出子问题的递推关系
• 确定 DP 数组的计算顺序
• 空间优化（可选）

这个解题步骤适用于任何一道动态规划题目，能够让你很快理清解题的各个要点。

图源来自 https://blog.csdn.net/feng_lin_hh/article/details/104483394

打家劫舍基本版

题目

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。

示例：

输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。

可以参考https://blog.csdn.net/qq_43568704/article/details/108062552 详解的非常详细。

题解

这里直接上代码。

/**
 * @param {number[]} nums
 * @return {number}
 */
var rob = function(nums) {
    
    const dp = [];   //设置常量可以减少运行时间
    if(nums.length === 0){
      return 0;
    };
     if(nums.length === 1){
      return nums[0];
    };
    //需要把dp[]数组的值都要初始化
    dp[0] = 0;
    dp[1] = nums[0];
    for(let i=2;i<=nums.length;i++){
       dp[i] =  Math.max(dp[i-1],dp[i-2]+nums[i-1])
    };
    return dp[nums.length]
};

斐波那契数列

// 计算斐波那契数列
/**
 * @param {number} n
 * @return {number}
 */
var fib = function(n) {
    var y = [];
    y[0] = 0;
    y[1] = 1;
    if(n === 0){
        return y[0];
    }
    if(n === 1){
        return y[1];
    }
    for(let i=2; i<=n; i++){
        y[i] = y[i-1] + y[i-2];
        y[i] %= 1000000007;               //答案要取模
    }
    return y[n];
};

对空间复杂度进行优化。得如下代码：

打家劫舍2

这里是对打家劫舍的一个升级，这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警 。

示例 1：

输入：nums = [2,3,2]
输出：3
解释：你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。

示例 2：

输入：nums = [1,2,3,1]
输出：4
解释：你可以先偷窃 1 号房屋（金额 = 1），然后偷窃 3 号房屋（金额 = 3）。
偷窃到的最高金额 = 1 + 3 = 4 。

示例 3：

输入：nums = [0]
输出：0

题解

思想就是将环状的分成两种情况，第一种不偷头房子，第二种不偷尾房子，这样的话就转换成了两个打家劫舍的基本版的问题。

/**
 * @param {number[]} nums
 * @return {number}
 */
//思想就是将环状的分成两种情况，第一种不偷头房子，第二种不偷尾房子，这样的话就转换成了两个打家劫舍的基本版的问题。
var rob = function (nums) {
  const n = nums.length;
  if (n === 1) return nums[0];
  return Math.max(
    robbing(nums.slice(0, n - 1)),
    robbing(nums.slice(1, n))
  );
};

// LeetCode 198   这段是别人写的打家劫舍基础版的代码
// function robbing(nums) {
//   const n = nums.length;
//   // 状态：dp[i]表示经历前i个房子能获取的最大价值
//   const dp = Array.from({ length: n + 1 }, () => 0);
//   // 迭代
//   for (let i = 1; i <= n; ++i) {
//     dp[i] = Math.max(
//       dp[i - 1], // 不偷i
//       nums[i - 1] + (i - 2 >= 0 ? dp[i - 2] : 0) // 偷i
//     );
//   }
//   // 目标
//   return dp[n];
// };

var robbing = function(nums) {
    
    const dp = [];   //设置常量可以减少运行时间
    if(nums.length === 0){
      return 0;
    };
     if(nums.length === 1){
      return nums[0];
    };
    //需要把dp[]数组的值都要初始化
    dp[0] = 0;
    dp[1] = nums[0];
    for(let i=2;i<=nums.length;i++){
       dp[i] =  Math.max(dp[i-1],dp[i-2]+nums[i-1])
    };
    return dp[nums.length]
};

信件错排

题目描述：有 N 个 信 和 信封，它们被打乱，求错误装信方式的数量。

定义一个数组 dp 存储错误方式数量，dp[i] 表示前 i 个信和信封的错误方式数量。假设第 i 个信装到第 j 个信封里面，而第 j 个信装到第 k 个信封里面。根据 i 和 k 是否相等，有两种情况：

• i==k，交换 i 和 j 的信后，它们的信和信封在正确的位置，但是其余 i-2 封信有 dp[i-2] 种错误装信的方式。由于 j 有 i-1 种取值，因此共有 (i-1)*dp[i-2] 种错误装信方式。
• i != k，交换 i 和 j 的信后，第 i 个信和信封在正确的位置，其余 i-1 封信有 dp[i-1] 种错误装信方式。由于 j 有 i-1 种取值，因此共有 (i-1)*dp[i-1] 种错误装信方式。

综上所述，错误装信数量方式数量为：

var MailMisalignment = function(int n){
        if(n==0) return 0;
        if(n==1) return 0;
        let dp = p[];
        dp[0] = 0;
        dp[1] = 1;
        for(int i=2;i<n;++i){
            dp[i] = (i-1)*dp[i-2] + (i-1)*dp[i-1];
        }
        return dp[n-1];
    }

母牛生产

[程序员代码面试指南-P181](HTTP://github.com/CyC2018/CS-Notes/blob/master/notes/Leetcode 题解 - 动态规划.md#)

题目描述：假设农场中成熟的母牛每年都会生 1 头小母牛，并且永远不会死。第一年有 1 只小母牛，从第二年开始，母牛开始生小母牛。每只小母牛 3 年之后成熟又可以生小母牛。给定整数 N，求 N 年后母牛的数量。

解析：利用动态规划（自己的思路不知道对不对）：

第一年： 1（只）

第二年：1（只）

第n年：成熟的牛=前一年成熟的牛的数量加上刚刚成熟的牛的数量

设d[n]为第n年母牛的数量，则d[n]等于第n-1年母牛的数量d[n-1]与第n年刚刚由小牛转为母牛的数量d[n-3]的和。（刚转化为母牛的数量为什么是d[n-3]呢，是因为这批刚成熟的小牛是由三年前成熟的母牛所生的，假设三年前所有母牛都正常生育且生一个的情况下。）

第 i 年成熟的牛的数量为：

function cow(n){
	if(n == 1 || n == 2){
          return 1;
    }	
	return cow(n - 1) + cow(n - 3);
}