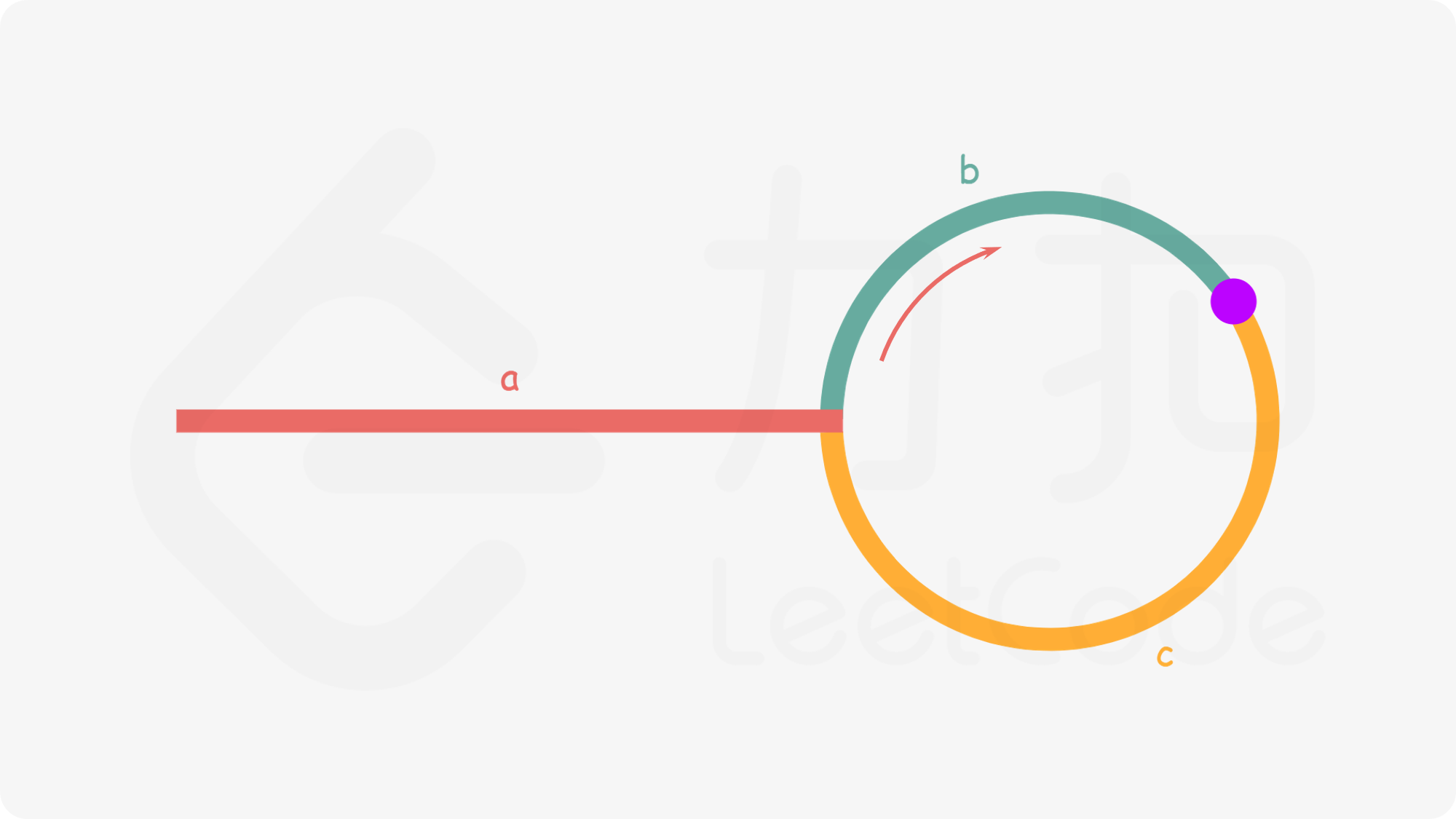链表类常见问题 无法高效获取长度,无法根据偏移快速访问元素 ,是链表的两个劣势。然而面试的时候经常碰见诸如获取倒数第k个元素 ,获取中间位置的元素 ,判断链表是否存在环 ,判断环的长度 等和长度与位置有关的问题。这些问题都可以通过灵活运用双指针 来解决。
Tips:双指针并不是固定的公式,而是一种思维方式 ~
先来看”倒数第k个元素的问题 “。设有两个指针 p 和 q,初始时均指向头结点。首先,先让 p 沿着 next 移动 k 次。此时,p 指向第 k+1个结点,q 指向头节点,两个指针的距离为 k 。然后,同时移动 p 和 q,直到 p 指向空,此时 q 即指向倒数第 k 个结点。
获取中间元素的问题 ,设有两个指针 fast 和 slow,初始时指向头节点。每次移动时,fast向后走两次,slow向后走一次,直到 fast 无法向后走两次。这使得在每轮移动之后。fast 和 slow 的距离就会增加一。设链表有 n 个元素,那么最多移动 n/2 轮。当 n 为奇数 时,slow 恰好指向中间结点 ,当 n 为 偶数 时,slow 恰好指向中间两个结点的靠前一个 (可以考虑下如何使其指向后一个结点呢?)。
是否存在环的问题 ,如果将尾结点的 next 指针指向其他任意一个结点,那么链表就存在了一个环。当一个链表有环时,快慢指针都会陷入环中进行无限次移动,然后变成了追及问题。想象一下在操场跑步的场景,只要一直跑下去,快的总会追上慢的。当两个指针都进入环后,每轮移动使得慢指针到快指针的距离增加一,同时快指针到慢指针的距离也减少一,只要一直移动下去,快指针总会追上慢指针。
输入一个链表,输出该链表中倒数第k个节点。为了符合大多数人的习惯,本题从1开始计数,即链表的尾节点是倒数第1个节点。
例如,一个链表有 6 个节点,从头节点开始,它们的值依次是 1、2、3、4、5、6。这个链表的倒数第 3 个节点是值为 4 的节点。
示例:
给定一个链表: 1->2->3->4->5, 和 k = 2.
返回链表 4->5.
题解 按照上面写的思路,快指针比慢指针往后多移k个,然后两个指针一起往后移动,直到快指针到达最后一个的next,为空为止,那么慢指针所指的便是倒数第k个节点之后的链表。
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 var getKthFromEnd = function (head, k ) let slow = head; let quick = head; while (k){ quick = quick.next; k--; } while (quick!==null ){ slow = slow.next; quick = quick.next; } return slow; };
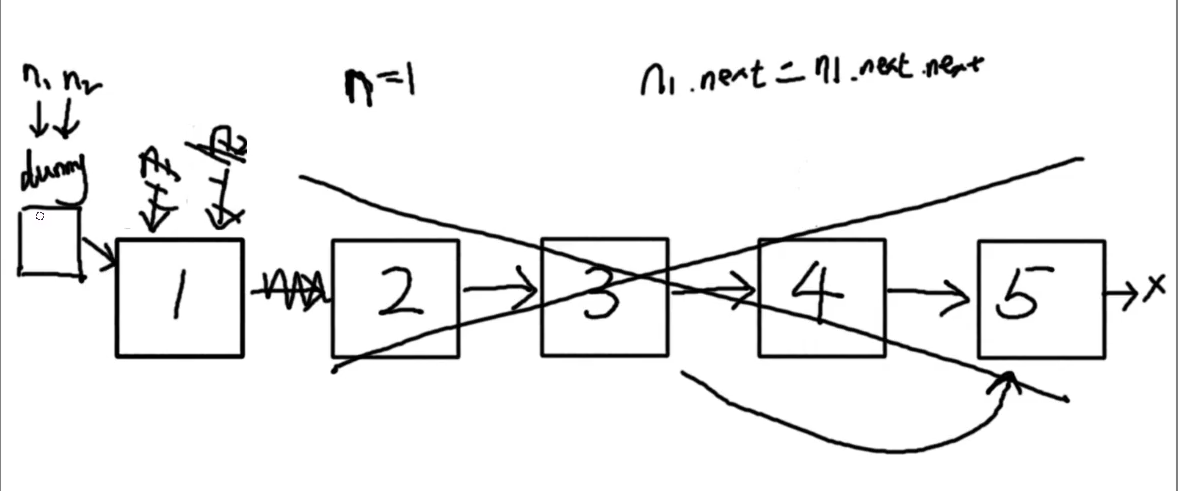
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
进阶:你能尝试使用一趟扫描实现吗?
示例 1:
输入:head = [1,2,3,4,5], n = 2
示例 2:
输入:head = [1], n = 1
示例 3:
输入:head = [1,2], n = 1
来源:力扣(LeetCode)
题解 双指针
dummyHead指向头指针head,将p,q指针都指向dummyHead移动快指针q,直至p,q之间相隔的节点个数为n
同时移动p,q,直到q的指针指向null,这个时候p指针的下一个节点即为所删除的节点
将p的next指向下下个节点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 var removeNthFromEnd = function (head, n ) let dumy = new ListNode(); dumy.next = head; let n1 = dumy; let n2 = dumy; for (i=0 ;i<n;i++){ n2 = n2.next; } while (n2.next!==null ){ n1 = n1.next; n2 = n2.next; } n1.next = n1.next.next; return dumy.next; };
给定一个头结点为 head 的非空单链表,返回链表的中间结点。
如果有两个中间结点,则返回第二个中间结点。
给定一个头结点为 head 的非空单链表,返回链表的中间结点。
如果有两个中间结点,则返回第二个中间结点。
示例 1:
1 2 3 4 5 输入:[1,2,3,4,5] 输出:此列表中的结点 3 (序列化形式:[3,4,5]) 返回的结点值为 3 。 (测评系统对该结点序列化表述是 [3,4,5])。 注意,我们返回了一个 ListNode 类型的对象 ans,这样: ans.val = 3, ans.next.val = 4, ans.next.next.val = 5, 以及 ans.next.next.next = NULL.
示例 2:
1 2 3 输入:[1,2,3,4,5,6] 输出:此列表中的结点 4 (序列化形式:[4,5,6]) 由于该列表有两个中间结点,值分别为 3 和 4,我们返回第二个结点。
题解 还是按照一开始写的方式,快指针一次移动两个,慢指针一次移动一个,直到快指针移到最后,那么慢指针到达的就是中点。这里注意,按照下面代码写的,如果链表长度为奇数时,慢指针刚好落到中点位置,如果长度为偶数时,慢指针落在中间两个数的后一个上。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 var middleNode = function (head ) let slow = head; let quick = head; while (quick!== null &&quick.next!==null ){ slow = slow.next; quick = quick.next.next; } return slow; };
当链表长度为偶数时如果想要慢指针落在两个中点数的前一个上,则可以在链表的前面再加一个节点,如下所示。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 var middleNode = function (head ) let dumy = new ListNode(); let slow = dumy; let quick = dumy; while (quick!== null &&quick.next!==null ){ slow = slow.next; quick = quick.next.next; } return slow; };
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例 1:
输入:l1 = [1,2,4], l2 = [1,3,4]
示例 2:
输入:l1 = [], l2 = []
示例 3:
输入:l1 = [], l2 = [0]
题解 1.递归(不是很熟,不太会用,但是注意递归一定要有终止条件)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 var mergeTwoLists = function (l1, l2 ) if (l1 === null ){ return l2; }else if (l2 === null ){ return l1; }else if (l1.val<=l2.val){ l1.next = (mergeTwoLists(l1.next,l2)); return l1; }else { l2.next = (mergeTwoLists(l1,l2.next)); return l2; } }
时间复杂度和空间复杂度都是O(n+m)
2.迭代
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 var mergeTwoLists = function (l1, l2 ) let prevNode = new ListNode(-1 ); let prev = prevNode; while (l1&&l2){ if (l1.val<=l2.val){ prev.next = l1; l1 = l1.next; }else { prev.next = l2; l2 = l2.next; } prev = prev.next; } prev.next = l1?l1:l2; return prevNode.next; };
题目可以跳转看一下。图太多….
题解 还是快慢指针,不多做赘述。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 var hasCycle = function (head ) if (!head||!head.next){ return false } let slow = head let fast = head while (fast!=null &&fast.next){ slow = slow.next fast = fast.next.next if (slow == fast){ return true } } return false };
和上一道题的差别是,这次要返回的是链表节点,就是入环节点索引的链表节点。(我也觉得有点绕!)
题解 第一种方法就是使用哈希表,把每一个节点都记录下来,直到遇到重复的节点返回即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 var detectCycle = function (head ) let set = new Set(); while(head!==null){ set .add(head); head = head.next; if(set .has(head)){ return head; } } return null ; };
第二种有点难理解,需要数学推导,这里先记住吧!
双指针: 我们使用两个指针,fast与 slow。它们起始都位于链表的头部。随后,slow指针每次向后移动一个位置,而 fast 指针向后移动两个位置。如果链表中存在环,则 fast 指针最终将再次与 slow指针在环中相遇。
如下图所示,设链表中环外部分的长度为 a。slow 指针进入环后,又走了 b 的距离与 fast 相遇。此时,fast 指针已经走完了环的 n 圈,因此它走过的总距离为 a+n(b+c)+b=a+(n+1)b+nc。
根据题意,任意时刻,fast 指针走过的距离都为 slow指针的 2 倍。因此,我们有
a+(n+1)b+nc=2(a+b) ⟹ a=c+(n−1)(b+c)
有了 a=c+(n−1)(b+c)的等量关系,我们会发现:从相遇点到入环点的距离加上 n−1 圈的环长,恰好等于从链表头部到入环点的距离。
因此,当发现 slow 与 fast相遇时,我们再额外使用一个指针 ptr。起始,它指向链表头部;随后,它和 slow 每次向后移动一个位置。最终,它们会在入环点相遇。
(这个公式说明a一定是n - 1圈加c的长度,这个时候,让ptr和慢指针同时+1着走, 那么慢指针走c之后,ptr到环入口的距离只剩整n - 1圈的距离了,而且此时慢指针也刚好走到入口处了, (因为我们无法确定c是多少,这个时候还得不出结论,那么:) 他俩一起走完n - 1圈的距离之后就会相遇,而且此时正好是入口)
自己用例子走了一遍,开始自己想的简单了,觉得快慢指针第一次相遇即为环的入口,原来并不是,利用数学推导发现规律,还需要再定义一个指针和慢指针接着走,相遇的点才是环的入口点。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 var detectCycle = function (head ) let slow = head; let quick = head; while (quick!==null &&quick.next!==null ){ slow = slow.next; quick = quick.next.next; if (quick === slow){ let ptr = head; while (ptr!==null ){ if (ptr == slow){ return ptr; } ptr = ptr.next; slow = slow.next; } } } return null ; };
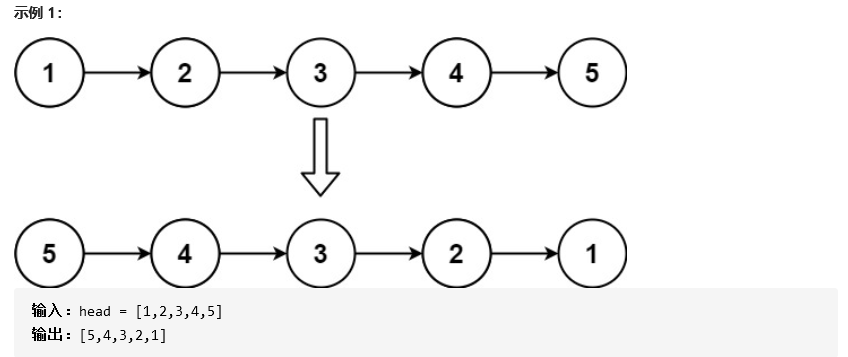
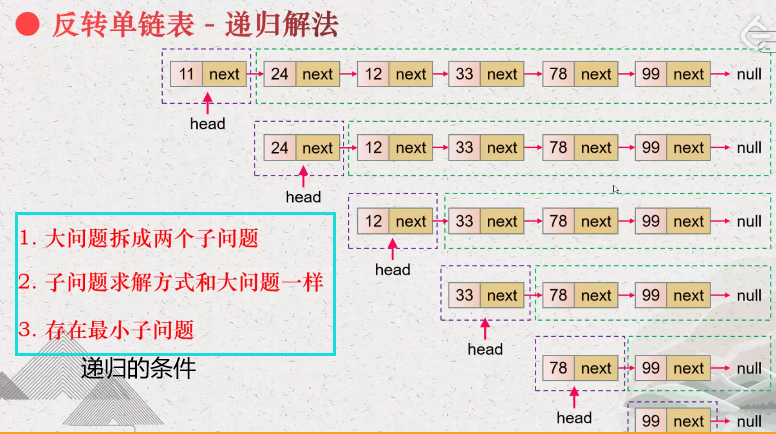
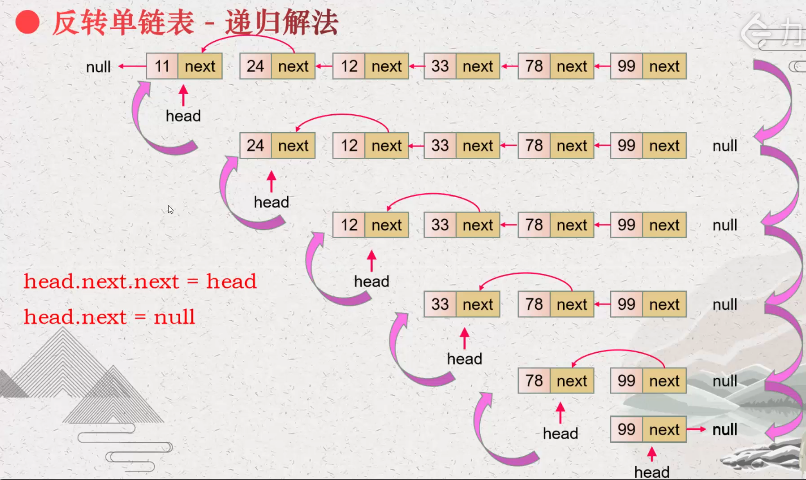
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
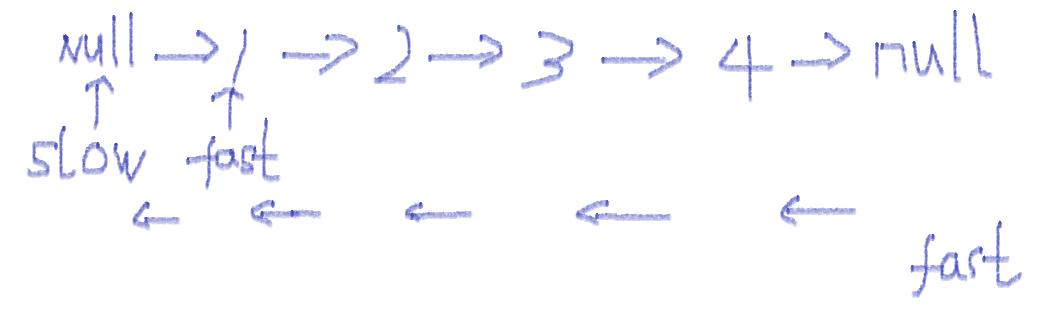
题解 1.使用双指针,这种解法也叫迭代法。慢指针先指向null,快指针指向head,然后先保存好快指针.next指针,再依次赋值往后推。
1 2 3 4 5 6 7 8 9 10 11 var reverseList = function (head ) let slow = null ; let fast = head; while (fast!==null ){ let next = fast.next; fast.next = slow; slow = fast; fast = next; } return slow; }
2.递归(递归我理解不了啊啊啊)
1 2 3 4 5 6 7 var reverseList = function (head ) if (head == null || head.next == null ) return head const p = reverseList(head.next) head.next.next = head head.next = null return p };
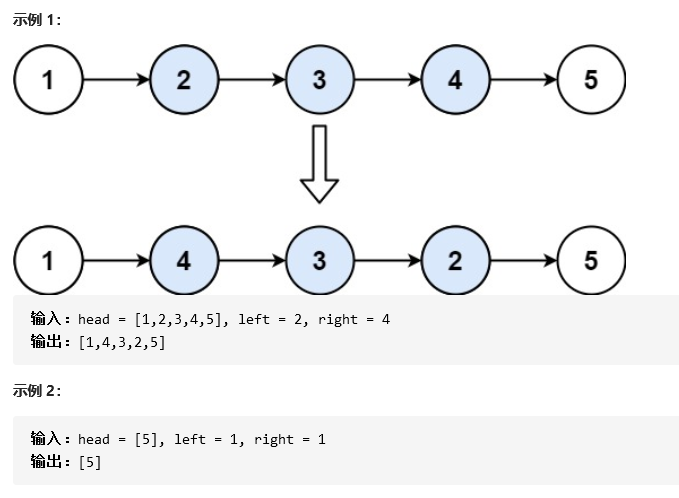
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。
题解 1.利用上一题的迭代法(将整个链表截断成三部分,中间部分为需要反转的链表,按照上题解法进行反转后再接起来)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 var reverseBetween = function (head, left, right ) const dummyNode = new ListNode(-1 ); dummyNode.next = head; let pre = dummyNode; for (let i = 0 ; i < left - 1 ; i++) { pre = pre.next; } let rightNode = pre; for (let i = 0 ; i < right - left + 1 ; i++) { rightNode = rightNode.next; } let leftNode = pre.next; let curr = rightNode.next; pre.next = null ; rightNode.next = null ; reverseLinkedList(leftNode); pre.next = rightNode; leftNode.next = curr; return dummyNode.next; }; const reverseLinkedList = (head ) => { let pre = null ; let cur = head; while (cur) { const next = cur.next; cur.next = pre; pre = cur; cur = next; } };
2.头插法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 var reverseBetween = function (head, left, right ) const dummy_node = new ListNode(-1 ); dummy_node.next = head; let pre = dummy_node; for (let i = 0 ; i < left - 1 ; ++i) { pre = pre.next; } let cur = pre.next; for (let i = 0 ; i < right - left; ++i) { const next = cur.next; cur.next = next.next; next.next = pre.next; pre.next = next; } return dummy_node.next; };
3.一次遍历(也是自己最开始想到的一种解法)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 var reverseBetween = function (head, left, right ) if (left == right) return head; let dummyHead = new ListNode(); dummyHead.next = head; let prev = dummyHead, curr = head; let i = 1 ; for (;i<left;i++) { prev = curr; curr = curr.next; } let tail = prev; let newTail = curr; tail.next = null ; prev = null ; for (;i<=right;i++) { let next = curr.next; curr.next = prev; prev = curr; curr = next; } newTail.next = curr; tail.next = prev; return dummyHead.next; };
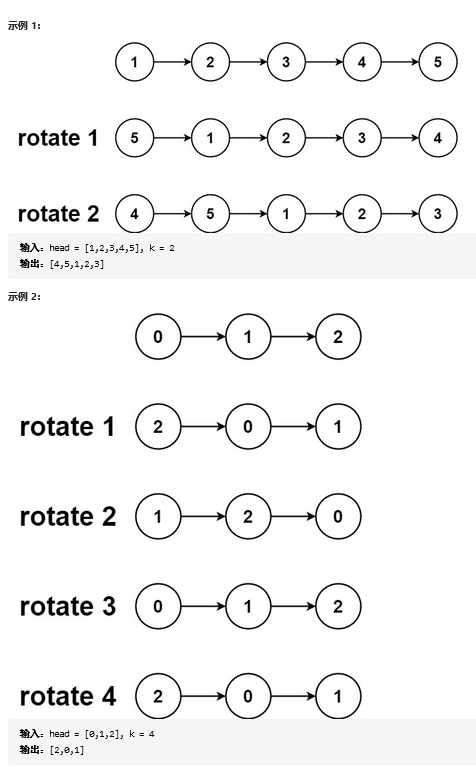
给你一个链表的头节点 head ,旋转链表,将链表每个节点向右移动 k 个位置。
题解 1.先把它转成环形链表,记录下链表的长度len,找到当k>len时该走到的位置后,断开该链表,即为旋转后的链表。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 var rotateRight = function (head, k ) if (head == null ||head.next == null ) return head; let len = 1 ; let prev = head; while (prev.next!==null ){ prev = prev.next; len = len+1 ; } let add = len - k%len; prev.next = head; while (add){ prev = prev.next; add--; } let ret = prev.next; prev.next = null ; return ret; };
2.快慢指针